GEOS SDK TechDocs|
| 
2.8 Polylines and Polygons | 
2.10 Drawing Bitmaps GrDrawCurve(), GrDrawCurveTo(), GrDrawSpline(), GrDrawSplineTo(), GrDrawRelCurveTo()
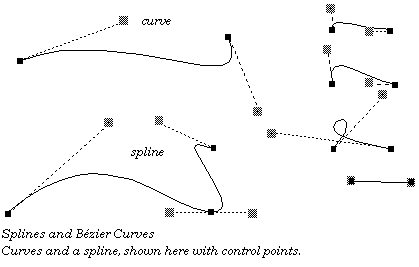
Bézier curves are mathematical constructs which provide a cheap and easy way to define smooth curves in a manner that computers can understand. There are other ways to define curves to computers, but the Bézier was chosen for the GEOS kernel because it is used in many standard font description formats. Splines, as implemented in GEOS, are created by drawing curves in sequence.
Bézier curves are defined in terms of four points. Two of these points are the endpoints, known as anchor points. The other two points are known as control points, one associated with each anchor point. The curve extends from anchor point to anchor point. The line between an anchor point and its control point determines the slope, or derivative, of the curve at the anchor point. The further the control point is from the anchor point, the further the curve wants to go along the straight line before curving off towards the other anchor point. A control point at zero distance from its anchor point won't affect the curve; if both control points are at zero distance from their anchors, the result will be a straight line segment.
GrDrawCurve()
draws a Bézier curve. It takes four points as arguments, using the first and last as anchor points and the middle two as control points.
GrDrawCurveTo()
draws a curve but uses the current pen position as the first anchor point, setting the pen position to the second anchor point after drawing.
It would be possible to draw splines by drawing a number of curves which had common endpoints, but the graphics system provides the
GrDrawSpline()
routine by which a spline with an arbitrary number of spline segments may be drawn with one call.
GrDrawSplineTo()
draws a spline with the current position as the first anchor point. The spline drawing routines require the application to set up an array of points. When calling
GrDrawSpline()
, these points should be in the order: anchor, control, control, anchor, control, control,..., anchor. The total number of points should be equal to 3n+1, where n is equal to the number of spline segments. Since
GrDrawSplineTo()
uses the current position as the first anchor point, for this function the array should start with the first control point, and there should be 3n points passed.
For most programmers, that's probably enough to know. Those programmers who want to know more and don't mind a bit of math may feel free to continue this section.
A curve is defined in terms of four points. There is a formula to determine the coordinates of all points on a spline in terms of these four points. The formula uses two parameterized cubic equations. These equations determine the x and y coordinates of a point on the curve. By finding the points corresponding to various parameters, it is possible to approximate the spline as closely as necessary. See below for the equations.
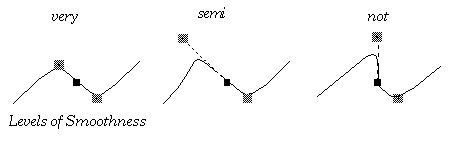
Splines may be created by drawing curves which share endpoints. Given an anchor point which two curves of a spline share, if the control point of one lies in the exact opposite direction of the other control point, the resulting spline will be smooth. If the control points are not only in the exact opposite directions but are also the same distance from the anchor point, then not only will the resulting spline be smooth, but its derivative will be smooth as well.
We call smooth splines with smooth derivatives "very smooth," and this condition is analogous to C'
continuity in functions. Smooth splines with non-smooth derivatives are called "semi smooth", analogous to G' continuity.
GEOS SDK TechDocs|
| 2.8 Polylines and Polygons | 2.10 Drawing Bitmaps